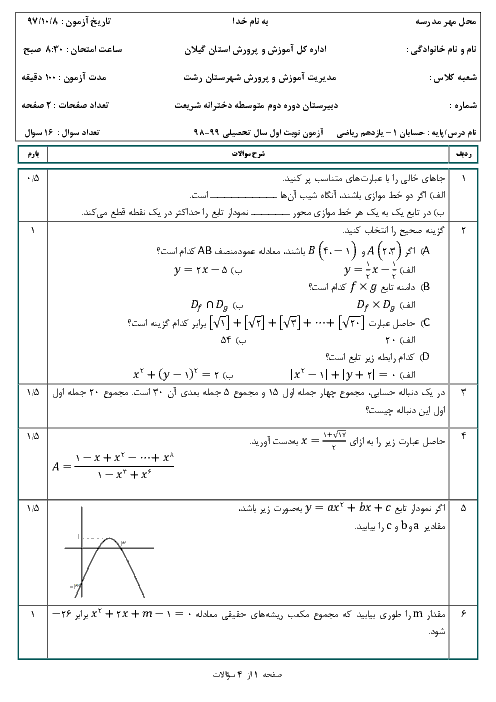
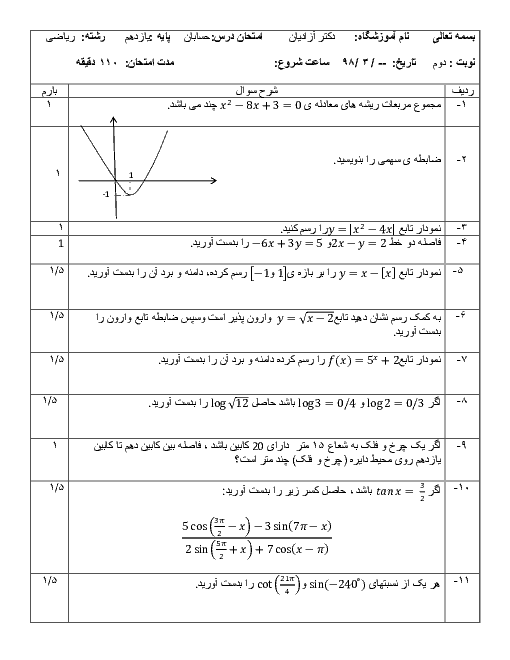
باتوجه به معادله داده شده می‌دانیم حاصل ضرب جواب های معادله برابر 2m-1 است.بنابراین:

$
\tan\mathit{\alpha}{\mathrm{.}}\cot\mathit{\alpha}\mathrm{{=}}{2}{m}\mathrm{{-}}{1}
$$
\mathrm{\Rightarrow}{1}\mathrm{{=}}{2}{m}\mathrm{{-}}{1}\mathrm{\Rightarrow}{m}\mathrm{{=}}{1}
$

حالا مجموع ریشه ها را بدست می‌آوریم بنا به رابطه خوانده شده مجموعه ریشه ها برابر m-3 است‌. پس:

$
\tan\mathit{\alpha}\mathrm{{+}}\cot\mathit{\alpha}\mathrm{{=}}{m}\mathrm{{-}}{3}\mathrm{{=}}{1}\mathrm{{-}}{3}\mathrm{{=}}\mathrm{{-}}{2}
$

دو طرف معادله را به توان2می رسانیم :

$
{\mathrm{(}}\tan\mathit{\alpha}\mathrm{{+}}\cot\mathit{\alpha}{\mathrm{)}}^{2}\mathrm{{=}}{4}\hspace{0.33em}
$$
\begin{array}{l}
{{\tan}^{2}\mathit{\alpha}\mathrm{{+}}{\cot}^{2}\mathit{\alpha}\mathrm{{+}}{2}\tan\mathit{\alpha}{\mathrm{.}}\cot\mathit{\alpha}}\\
{\mathrm{{=}}{4}}
\end{array}
$$
\begin{array}{l}
{{\mathrm{(}}\tan\mathit{\alpha}\mathrm{{+}}\cot\mathit{\alpha}{\mathrm{)}}^{2}\mathrm{{=}}{4}\hspace{0.33em}}\\
{\hspace{0.33em}\mathrm{\Rightarrow}{\tan}^{2}\mathit{\alpha}\mathrm{{+}}{\cot}^{2}\mathit{\alpha}\mathrm{{+}}{2}\mathrm{{=}}{4}}
\end{array}
$
$
\mathrm{\Rightarrow}{\tan}^{2}\mathit{\alpha}\mathrm{{+}}{\cot}^{2}\mathit{\alpha}\mathrm{{=}}{2}
$