ابتدا فرض می‌کنیم که بار ${{q}_{3}}$ در نقطهٔ A قرار داشته باشد:
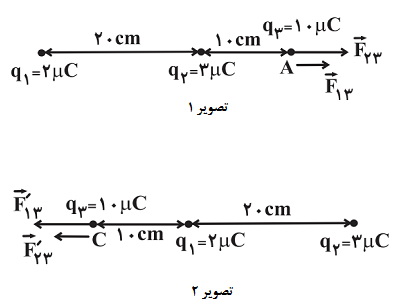
با توجه به تصویر 1

$\begin{align}
  & F=k\frac{\left| q \right|\left| {{q}_{3}} \right|}{{{r}^{2}}} \\
 & \left. \begin{matrix}
   {{F}_{13}}=9\times {{10}^{9}}\times \frac{2\times {{10}^{-6}}\times 10\times {{10}^{-6}}}{{{(30\times {{10}^{-2}})}^{2}}}=2N  \\
   {{F}_{23}}=9\times {{10}^{9}}\times \frac{3\times {{10}^{-6}}\times 10\times {{10}^{-6}}}{{{(10\times {{10}^{-2}})}^{2}}}=27N  \\
\end{matrix} \right\}\Rightarrow {{F}_{A}}={{F}_{13}}+{{F}_{23}}=29N \\
\end{align}$

حال فرض می‌کنیم که بار ${{q}_{3}}$ در نقطهٔ C قرار داشته باشد:
با توجه تصویر 2

$\begin{align}
  & \left. \begin{matrix}
   {{{{F}'}}_{13}}=9\times {{10}^{9}}\times \frac{2\times {{10}^{-6}}\times 10\times {{10}^{-6}}}{{{(10\times {{10}^{-2}})}^{2}}}=18N  \\
   {{{{F}'}}_{23}}=9\times {{10}^{9}}\times \frac{3\times {{10}^{-6}}\times 10\times {{10}^{-6}}}{{{(30\times {{10}^{-2}})}^{2}}}=3N  \\
\end{matrix} \right\}\Rightarrow {{F}_{C}}={{{{F}'}}_{13}}+{{{{F}'}}_{23}}=21N \\
 & \frac{{{F}_{C}}}{{{F}_{A}}}=\frac{21}{29} \\
\end{align}$