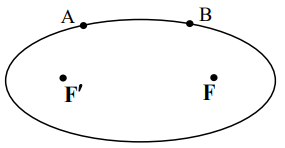
در شکل زیر دو نقطه A و B روی بیضی با کانون‌های F و ${F'}$ قرار دارند. اگر $AF' = BF$ و همچنین AF و $BF'$ یکدیگر را درون بیضی در نقطه‌ای مانند M قطع کنند، نشان دهید: مثلث $FMF'$ متساوی الساقین است و M روی قطر کوچک بیضی قرار دارد.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...