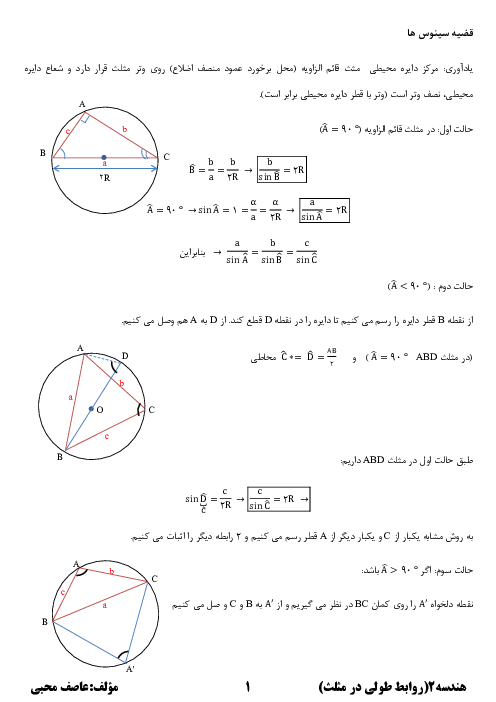
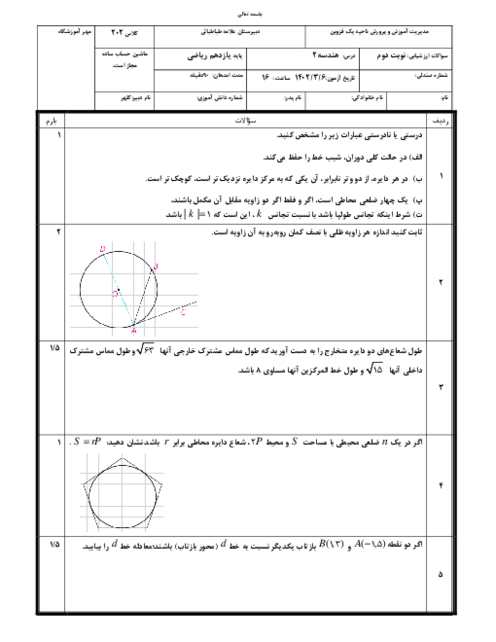
درس 3: قضیۀ نیمسازهای زوایای داخلی و محاسبۀ طول نیمسازها
هندسه (2)
یازدهم
متوسطه دوم نظری
علوم ریاضی
درسنامه آموزشی این مبحث
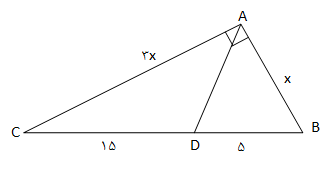
در يك مثلث قائمالزاويه، نيمساز زاويهی قائمه روی وتر قطعاتی بهطولهای 5 و 15 ايجاد كرده است. مساحت اين مثلث چقدر است؟