رأس سهمی به معادلهٔ بر روی خط به معادلهٔ قرار دارد. این سهمی از کدام نقطهٔ زیر می‌گذرد؟ | ریاضی و آمار (1) دهم شماره 245889 - گاما

گاما رو نصب کن!

درحال دریافت اطلاعات ...

{{ successMsg }}

{{ errorMsg }}

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

ورود با رمزعبور

برای استفاده بسیاری از امکانات گاما و خیلی از وبسایت ها باید جاوا اسکریپت را در مرورگر خود فعال کنید.

برای این کار باید به تنظیمات مرورگر خود مراجعه کنید.

جستجو

پربازدیدها: #{{ tag.title }}

نمونه سوال

فایل آموزشی

پرسش و پاسخ

آزمون آنلاین

درسنامه آموزشی

مدرسه یاب

جستجوهای پرتکرار

نوبت اول گام به گام کاربرگ آزمون عملکردی پودمان آزمون پیشرفت تحصیلی طرح درس نمونه سوال تست پاورپوینت علوم هشتم فارسی چهارم ریاضی هفتم علوم نهم گزارش کارورزی

نمونه سوال

محتوای آموزشی

آزمون آنلاین

پرسش و پاسخ

درسنامه آموزشی

مدرسه یاب

معلم خصوصی

فرم معتبر نیست.

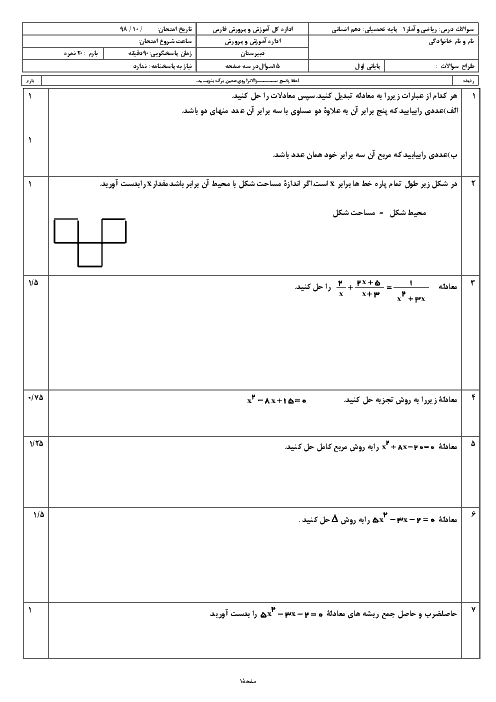
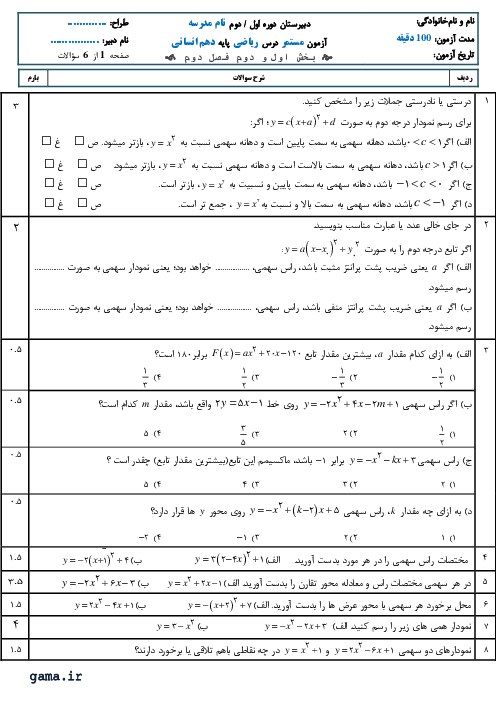
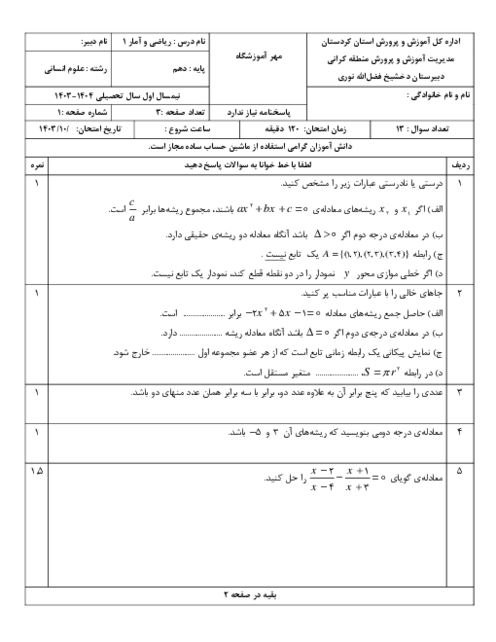
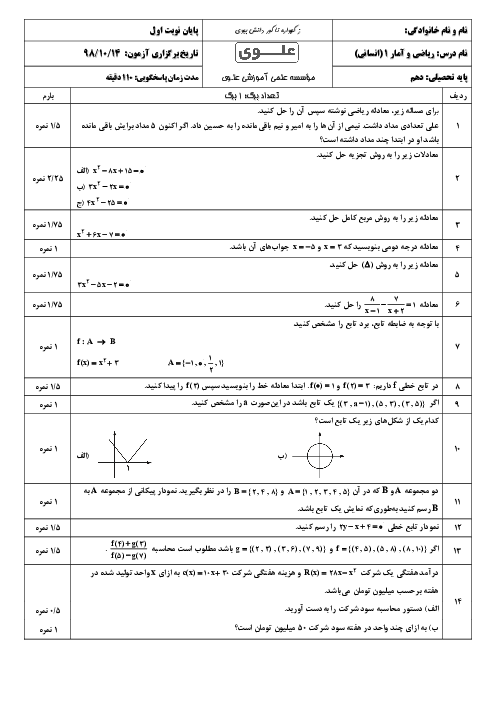
درس 4: رسم تابع درجۀ 2 ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری ادبیات و علوم انسانی درسنامه آموزشی این مبحث

رأس سهمی به معادلهٔ $y = - {x^2} + ax + 5$ بر روی خط به معادلهٔ $x = 2$ قرار دارد. این سهمی از کدام نقطهٔ زیر می‌گذرد؟

1 )

$(1,8)$

2 )

$( - 1,5)$

3 )

$( - 1,4)$

4 )

$(1,9)$

نمایش پاسخ

رأس سهمی روی خط به معادلهٔ $x = 2$ قرار دارد که همان طول رأس سهمی است، حال داریم:

$y = - {x^2} + ax + 5 \to y = a'{x^2} + b'x + c' \to $

$\eqalign{
& a' = - 1 \cr
& b' = a \cr
& c' = 5 \cr} $

طول رأس سهمی ${x_v} = \frac{{ - b'}}{{2a'}} \to {x_v} = 2 \to 2 = \frac{{ - a}}{{2 \times ( - 1)}} \Rightarrow 2 = \frac{a}{2} \Rightarrow a = 4$

پس معادلهٔ سهمی به‌صورت $y = - {x^2} + 4x + 5$ است، حال با توجه به گزینه‌ها به ازای $x = 1$ و $x = - 1$ مقدار $y$ را به‌دست می‌آوریم:

$y = - {x^2} + 4x + 5$

$y = {( - 1)^2} + 4( - 1) + 5 = - 1 - 4 + 5 = 0 \Rightarrow ( - 1,0)$

$y = - {(1)^2} + 4 \times (1) + 5 = - 1 + 4 + 5 = 8 \Rightarrow (1,8)$

با توجه به گزینه‌ها، گزینهٔ «1» صحیح است.

گزارش اشکال

یک تست دیگه بزن

یک آزمون کامل بده

تحلیل ویدئویی تست

1401/12/10

ندا تقوی

1401/07/26

عادل علی پناه

ویدیو دوره آموزشی، ریاضی و آمار (1) دهم دوره دوم متوسطه- نظری

مدرس: سعید شریفی

مدت دوره: 7 ساعت (8 فایل)

با گنجینه سوال، آزمون دلخواهتو بساز

ترند شده

امتحان میان ترم دوم ریاضی و آمار (1) دهم دبیرستان حضرت معصومه | فصل 1 تا 3

4 صفحه

امتحان میان ترم دوم ریاضی و آمار (1) دهم دبیرستان حضرت معصومه | فصل 1…

سکینه باقری فرد

سوالات امتحان جبرانی نوبت دوم ریاضی و آمار (1) پایه دهم دبیرستان حافظ | شهریور 1397

2 صفحه

سوالات امتحان جبرانی نوبت دوم ریاضی و آمار (1) پایه دهم دبیرستان حافظ…

سید امید حسینی

سوالات آزمون نوبت دوم ریاضی و آمار (1) دهم دبیرستان شیخ فضل الله نوری | خرداد 1401

6 صفحه

سوالات آزمون نوبت دوم ریاضی و آمار (1) دهم دبیرستان شیخ فضل الله نوری…

محمدجواد باغبان باشی

رایـــــگان

سوالات مرحله اول نهمین دوره مسابقه تورنی تیم ریاضی پایۀ دهم انسانی | بهمن 96

8 صفحه

سوالات مرحله اول نهمین دوره مسابقه تورنی تیم ریاضی پایۀ دهم انسانی | بهمن…

مسابقه تورونی تیم

رایـــــگان

سوالات مرحله اول دهمین دوره مسابقه تورنی تیم ریاضی پایۀ دهم انسانی | آذر 97

8 صفحه

سوالات مرحله اول دهمین دوره مسابقه تورنی تیم ریاضی پایۀ دهم انسانی | آذر…

مسابقه تورونی تیم

رایـــــگان

آزمون نوبت اول ریاضی و آمار (1) دهم دبیرستان الغدیر | دی 1395

2 صفحه

آزمون نوبت اول ریاضی و آمار (1) دهم دبیرستان الغدیر | دی 1395

وحید مختاری

سوالات مفهومی امتحان نوبت اول ریاضی و آمار 1 دبیرستان شهید هاشمی نژاد دی 1403

5 صفحه

سوالات مفهومی امتحان نوبت اول ریاضی و آمار 1 دبیرستان شهید هاشمی نژاد…

مجتبی محمدیان

آزمون ریاضی و آمار (1) دهم دبیرستان شیخ فضل الله نوری | فصل اول (درس 1 و 2: مسائل توصیفی و حل معادله درجه 2)

4 صفحه

آزمون ریاضی و آمار (1) دهم دبیرستان شیخ فضل الله نوری | فصل اول (درس 1…

محمدجواد باغبان باشی

امتحان ترم اول ریاضی و آمار (1) دهم دبیرستان غیردولتی پگاه | دی 1399

3 صفحه

امتحان ترم اول ریاضی و آمار (1) دهم دبیرستان غیردولتی پگاه | دی 1399

رهام کمندی

امتحان نوبت اول ریاضی و آمار دهم دبیرستان امام رضا | دی 1397

2 صفحه

امتحان نوبت اول ریاضی و آمار دهم دبیرستان امام رضا | دی 1397

رضا جوانمردی

موارد بیشتر

موارد بیشتر

ارسال فایل

مسئله ما و ما و نصفه‌ای از نصف ما گر توهم با ما شوی ما جملگی صد می‌شویم. را بنویسید.

ریشه معادله درجه دومی رادیکال 3-1 و رادیکال 3-1 است. معادله آن کدام است؟

مجموع دو عدد زوج متوالی 46 است. آن دو عدد را بدست آورید.

موارد بیشتر

ارسال پرسش

موارد بیشتر