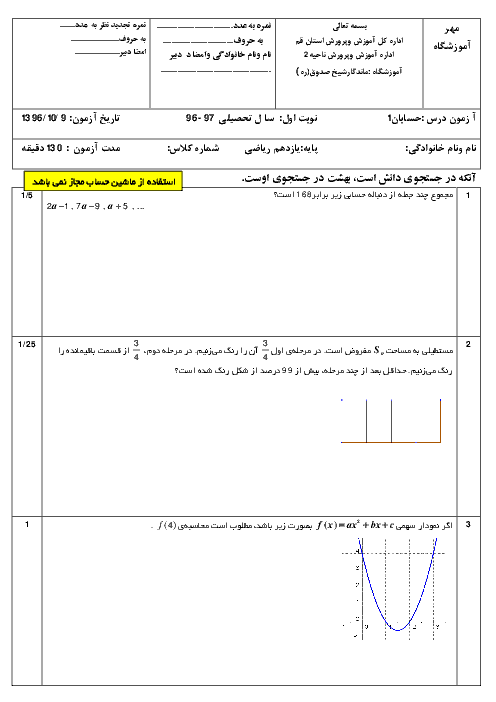
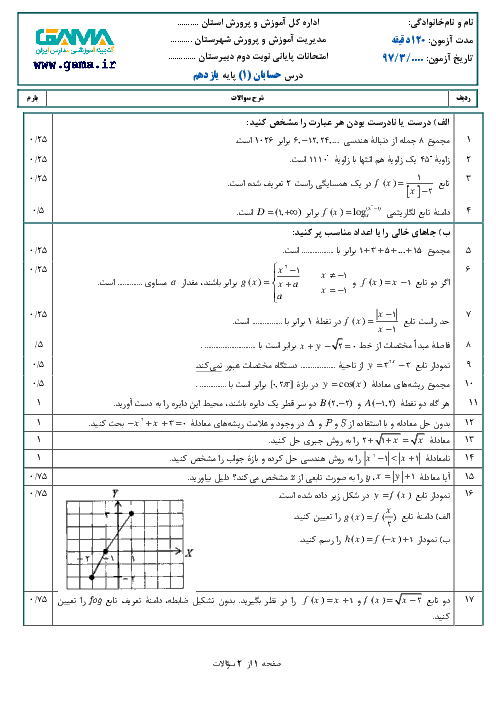
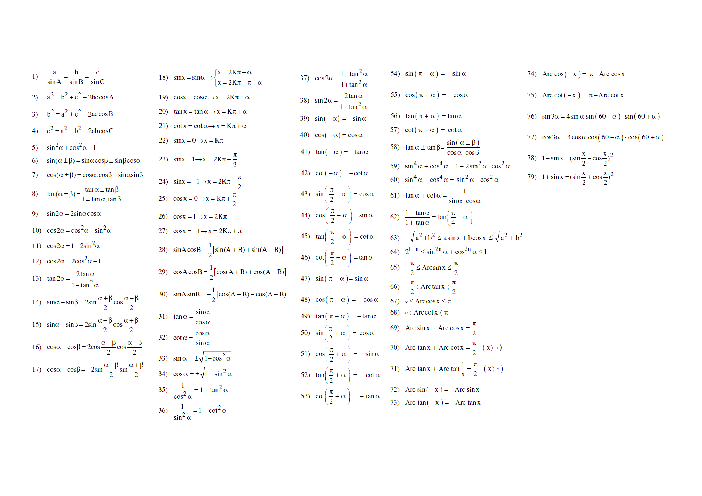
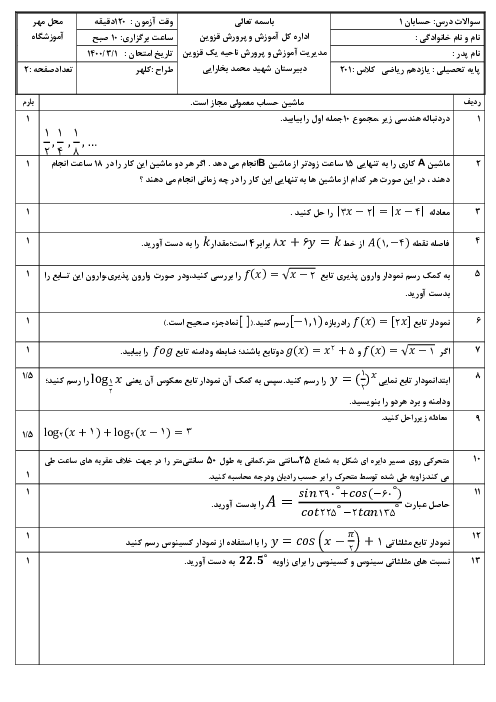
اگر تابع $f(x) = \left\{ {\begin{array}{*{20}{c}} {\sqrt {2{x^2} - 4a} }&{x \geqslant 2} \\ {x + b}&{ - 2 \leqslant x < 2} \\ {x^2} + bx + 3a&{x < -2} \\ \end{array}} \right.$ باشد b و a را طوری بیابید که تابع f در نقطهٔ $x = - 2$ دارای حد بوده و $\mathop {Lim}\limits_{x \to {2^ + }} f(x) = 2$ باشد.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...